Producing Random Numbers in R

Whether or not engaged on a machine studying venture, a simulation, or different fashions, you want to generate random numbers in your code. R as a programming language, has a number of capabilities for random quantity technology. On this put up, you’ll study them and see how they can be utilized in a bigger program. Particularly, you’ll study

• Find out how to generate Gaussian random numbers right into a vector
• Find out how to generate uniform random numbers
• Find out how to manipulate random vectors and random matrices

Let’s get began.

Producing Random Numbers in R.
Picture by Kaysha. Some rights reserved.

Overview

This put up is split into three components; they’re:

• Random Quantity Turbines
• Correlated Multivariate Gaussian Random Quantity
• Producing Random Numbers From Uniform Distribution

Random Quantity Turbines

Random numbers are drawn from likelihood distributions. Probably the most well-known distribution ought to be the Gaussian distribution, often known as the traditional distribution.

The usual regular distribution is outlined by its density operate, $f(x) = (2pi)^{-1/2} exp(-x^2/2)$. It has a variety of the whole actual quantity, i.e., from damaging infinity to constructive infinity. Integrating $f(x)$ over this vary offers the end result 1.0. In arithmetic, we now have the distribution operate $F(x) = int_{-infty}^x (2pi)^{-1/2} exp(-t^2/2) dt$ outlined because the likelihood {that a} quantity is beneath $x$ in the usual regular distribution.

In R, you haven’t solely the random quantity generator operate primarily based on the usual regular distribution however a number of different auxiliary capabilities as properly:

• dnorm(x): The density operate $f(x)$
• pnorm(x): The distribution operate $F(x)$
• qnorm(x): The quantile operate $F^{-1}(x)$ because the inverse operate of $F(x)$
• rnorm(ok): The random quantity generator operate

The capabilities dnorm(x), pnorm(x), qnorm(x) could be helpful in some tasks that you want to take care of another likelihood distribution. The operate rnorm(ok) is the operate that provides you a vector of ok random values which might be drawn from the usual regular distribution. That is the operate you employ most frequently.

You may inform that that is the random quantity generator that produces output from the usual regular distribution by getting plenty of samples from it and plot a histogram:

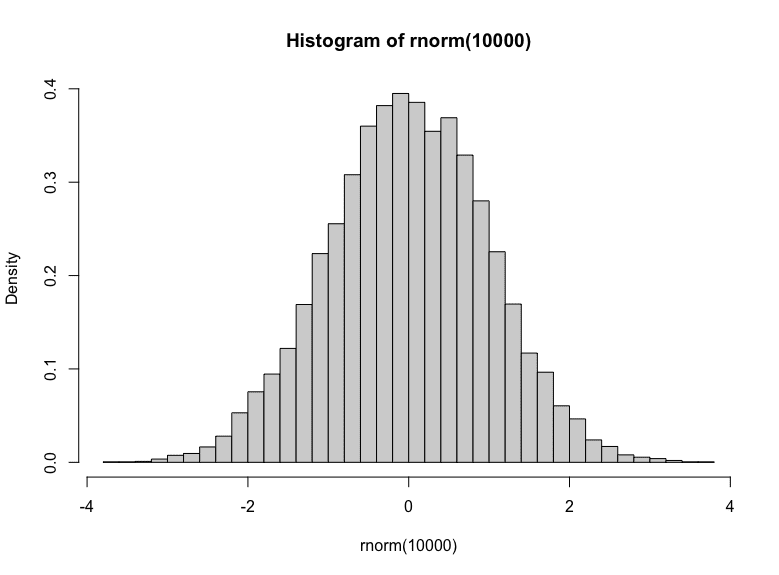
Histogram of Gaussian random numbers

You may see a bell-shaped histogram centered at zero within the plot. Additionally, you may inform that majority of the samples are between -1 to +1 (68% of them, to be exact). The freq=FALSE parameter within the hist() operate makes the $y$-axis in density as a substitute of frequency. Therefore you may match the histogram with the density operate.

Correlated Multivariate Gaussian Random Quantity

One frequent use case of ordinary regular random quantity generator is to create pairs of correlated Gaussian random quantity. In different phrases, you need some bivariate Gaussian random numbers with non-zero correlation.

The algorithm to generate such correlated random numbers is:

1. First, generate identical variety of impartial normal regular random numbers
2. Arrange the covariance matrix to specify how the completely different random numbers are associated
3. Take the Cholesky decomposition of the covariance matrix
4. Multiply the matrix of impartial normal regular random numbers with the Cholesky decomposition matrix
5. Optionally, modify the imply

In code, it’s:

A lot of the code above is intuitive. The difficult half is adjusting the imply: Commonplace Gaussian random numbers are centered at zero. The Cholesky decomposition matrix obtained from the road cholesky <- chol(cov) can solely modify the covariance with out adjusting the imply. To shift the imply worth, you want to add a price uniformly on every column. Within the above, you repeat the vector right into a matrix of the identical form because the random commentary so you may add them.

How one can inform that is appropriate? A technique is to confirm the statistics. You may compute and print the correlation matrix, the column imply, and column normal deviation as follows:

These three traces ought to print the empirical correlation matrix, the imply, and the usual deviation respectively. You can too attempt to plot the random numbers as a scatter plot:

Which ought to appear like the next:

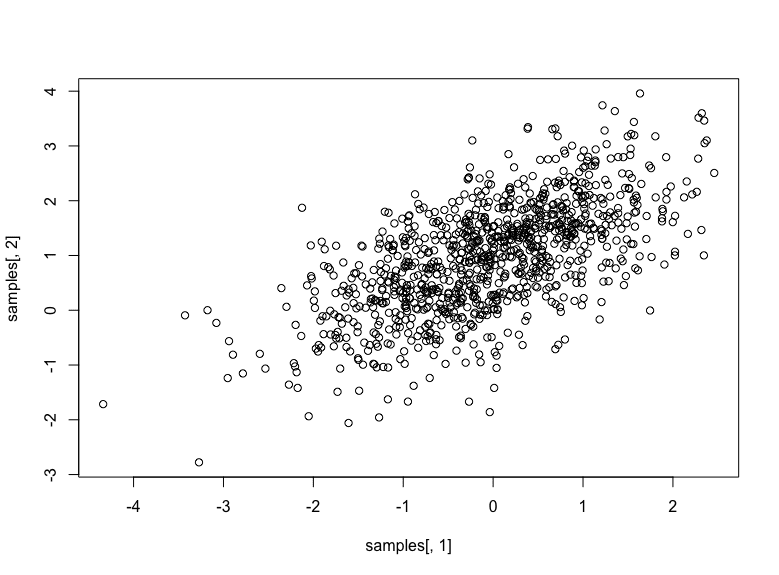
Bivariate Gaussian random numbers with imply at (0,1) and correlation 0.6

Placing every part collectively, the next is the entire code:

Producing Random Numbers From Uniform Distribution

Gaussian is probably the most used distribution. However there are probabilities that you will want a unique distribution. One instance is to simulate the arrival time of the following telephone name on a hotline. It is a basic instance of the exponential distribution. Clearly, it’s not Gaussian since Gaussian random values could be damaging.

The exponential distribution has a density operate $f(x) = lambda exp(-lambda x)$. Since $x$ runs from zero to constructive infinity, the distribution operate is $F(x) = 1-exp(-lambda x)$. Recall {that a} distribution operate has a price between 0 and 1.

With an arbitrary distribution operate, you should use the inverse remodel sampling technique to generate random numbers utilizing a uniform distribution. The thought is that you would be able to take into account $F(x)$ as the usual uniform distribution. Then you may lookup the worth of $x$ because the generated random quantity. On this case, you want to outline the inverse of the distribution operate $F^{-1}(x)$.

The inverse operate in exponential distribution is trivial: Set $y = 1 – exp(-lambda x)$, then $x = -log(1-y)/lambda$. Therefore $F^{-1}(x) = -log(1-y)/lambda$. In R, you may generate exponential distributed random numbers as follows:

Within the above, you used not rnorm() operate however runif() operate for a uniform distribution between 0 and 1. There are a complete set of capabilities for uniform distribution, too, corresponding to dunif() and punif().

You is aware of the generated numbers follows an exponential distribution when you plot the histogram from the generated numbers:

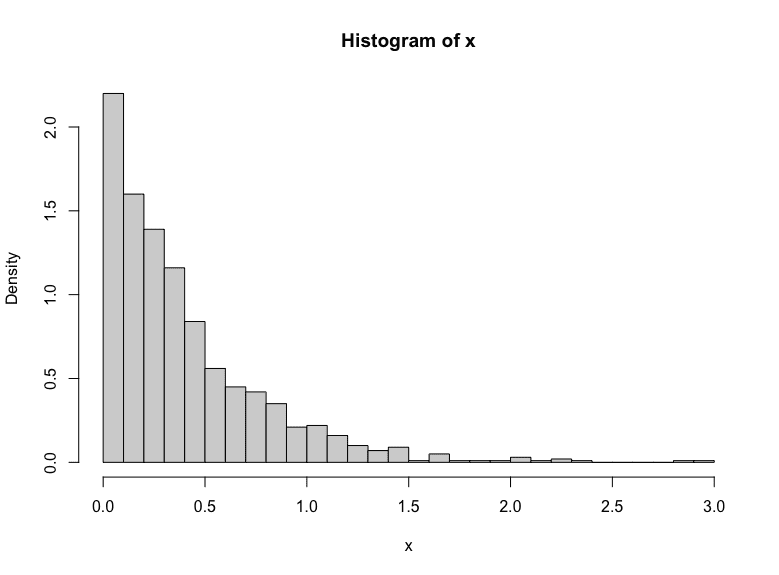
Exponential distribution generated empirically.

This system could be helpful whenever you construct a discrete occasion simulation mannequin in R.

Additional Readings

You may study extra concerning the above subjects from the next:

Web site

Abstract

On this put up, you discovered how one can generate random numbers in R. Particularly, you discovered:

• The suite of capabilities in R for likelihood distributions and random quantity technology
• Find out how to create random numbers in Gaussian distribution
• Find out how to create random numbers in uniform distribution
• Find out how to make use of the random quantity mills to create multivariate Gaussian distribution or different distribution utilizing the inverse remodel technique.