Deep neural networks have enabled technological wonders starting from voice recognition to machine transition to protein engineering, however their design and utility is nonetheless notoriously unprincipled.
The event of instruments and strategies to information this course of is without doubt one of the grand challenges of deep studying concept.
In Reverse Engineering the Neural Tangent Kernel, we suggest a paradigm for bringing some precept to the artwork of structure design utilizing latest theoretical breakthroughs: first design kernel perform – usually a a lot simpler job – after which “reverse-engineer” a net-kernel equivalence to translate the chosen kernel right into a neural community.
Our predominant theoretical end result allows the design of activation features from first rules, and we use it to create one activation perform that mimics deep (textrm{ReLU}) community efficiency with only one hidden layer and one other that soundly outperforms deep (textrm{ReLU}) networks on an artificial job.
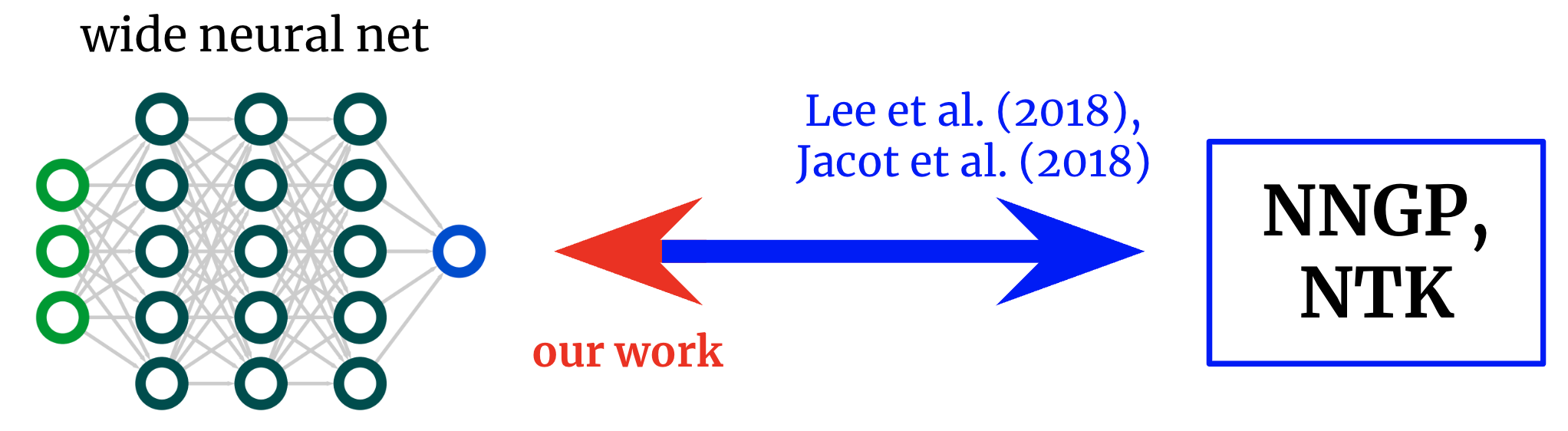
Kernels again to networks. Foundational works derived formulae that map from large neural networks to their corresponding kernels. We get hold of an inverse mapping, allowing us to start out from a desired kernel and switch it again right into a community structure.
Neural community kernels
The sector of deep studying concept has not too long ago been remodeled by the conclusion that deep neural networks usually turn out to be analytically tractable to check within the infinite-width restrict.
Take the restrict a sure approach, and the community actually converges to an atypical kernel technique utilizing both the structure’s “neural tangent kernel” (NTK) or, if solely the final layer is skilled (a la random function fashions), its “neural community Gaussian course of” (NNGP) kernel.
Just like the central restrict theorem, these wide-network limits are sometimes surprisingly good approximations even removed from infinite width (usually holding true at widths within the tons of or hundreds), giving a outstanding analytical deal with on the mysteries of deep studying.
From networks to kernels and again once more
The unique works exploring this net-kernel correspondence gave formulae for going from structure to kernel: given an outline of an structure (e.g. depth and activation perform), they provide the community’s two kernels.
This has allowed nice insights into the optimization and generalization of varied architectures of curiosity.
Nevertheless, if our objective just isn’t merely to know present architectures however to design new ones, then we would reasonably have the mapping within the reverse path: given a kernel we wish, can we discover an structure that offers it to us?
On this work, we derive this inverse mapping for fully-connected networks (FCNs), permitting us to design easy networks in a principled method by (a) positing a desired kernel and (b) designing an activation perform that offers it.
To see why this is smart, let’s first visualize an NTK.
Take into account a large FCN’s NTK (Ok(x_1,x_2)) on two enter vectors (x_1) and (x_2) (which we’ll for simplicity assume are normalized to the identical size).
For a FCN, this kernel is rotation-invariant within the sense that (Ok(x_1,x_2) = Ok(c)), the place (c) is the cosine of the angle between the inputs.
Since (Ok(c)) is a scalar perform of a scalar argument, we will merely plot it.
Fig. 2 exhibits the NTK of a four-hidden-layer (4HL) (textrm{ReLU}) FCN.
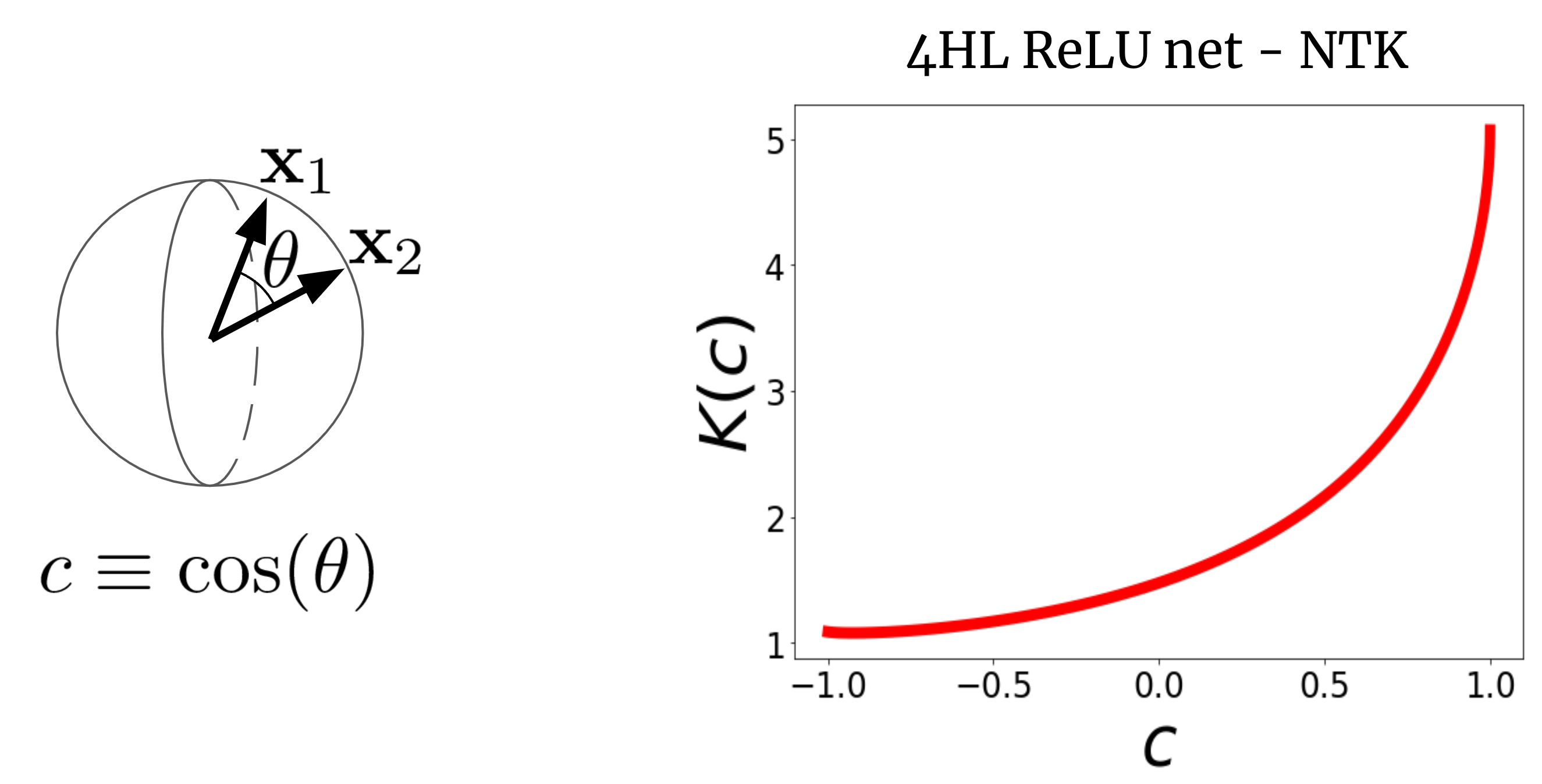
Fig 2. The NTK of a 4HL $textrm{ReLU}$ FCN as a perform of the cosine between two enter vectors $x_1$ and $x_2$.
This plot really accommodates a lot details about the educational conduct of the corresponding large community!
The monotonic enhance signifies that this kernel expects nearer factors to have extra correlated perform values.
The steep enhance on the finish tells us that the correlation size just isn’t too giant, and it could actually match difficult features.
The diverging spinoff at (c=1) tells us in regards to the smoothness of the perform we count on to get.
Importantly, none of those info are obvious from taking a look at a plot of (textrm{ReLU}(z))!
We declare that, if we need to perceive the impact of selecting an activation perform (phi), then the ensuing NTK is definitely extra informative than (phi) itself.
It thus maybe is smart to attempt to design architectures in “kernel area,” then translate them to the standard hyperparameters.
An activation perform for each kernel
Our predominant result’s a “reverse engineering theorem” that states the next:
Thm 1: For any kernel $Ok(c)$, we will assemble an activation perform $tilde{phi}$ such that, when inserted right into a single-hidden-layer FCN, its infinite-width NTK or NNGP kernel is $Ok(c)$.
We give an specific method for (tilde{phi}) when it comes to Hermite polynomials
(although we use a distinct useful type in apply for trainability causes).
Our proposed use of this result’s that, in issues with some recognized construction, it’ll generally be potential to put in writing down kernel and reverse-engineer it right into a trainable community with numerous benefits over pure kernel regression, like computational effectivity and the power to study options.
As a proof of idea, we check this concept out on the artificial parity drawback (i.e., given a bitstring, is the sum odd and even?), instantly producing an activation perform that dramatically outperforms (textual content{ReLU}) on the duty.
One hidden layer is all you want?
Right here’s one other shocking use of our end result.
The kernel curve above is for a 4HL (textrm{ReLU}) FCN, however I claimed that we will obtain any kernel, together with that one, with only one hidden layer.
This means we will give you some new activation perform (tilde{phi}) that offers this “deep” NTK in a shallow community!
Fig. 3 illustrates this experiment.
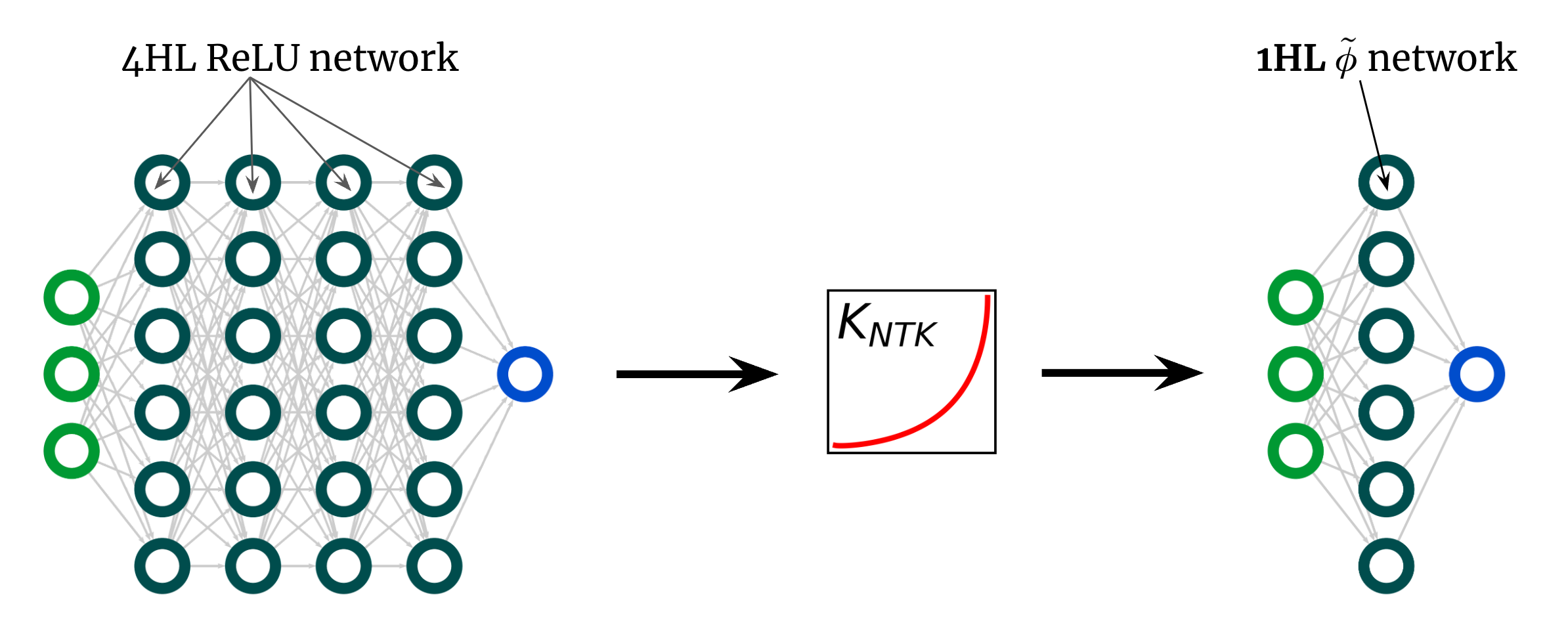
Fig 3. Shallowification of a deep $textrm{ReLU}$ FCN right into a 1HL FCN with an engineered activation perform $tilde{phi}$.
Surprisingly, this “shallowfication” really works.
The left subplot of Fig. 4 beneath exhibits a “mimic” activation perform (tilde{phi}) that offers nearly the identical NTK as a deep (textrm{ReLU}) FCN.
The fitting plots then present practice + check loss + accuracy traces for 3 FCNs on an ordinary tabular drawback from the UCI dataset.
Notice that, whereas the shallow and deep ReLU networks have very totally different behaviors, our engineered shallow mimic community tracks the deep community nearly precisely!
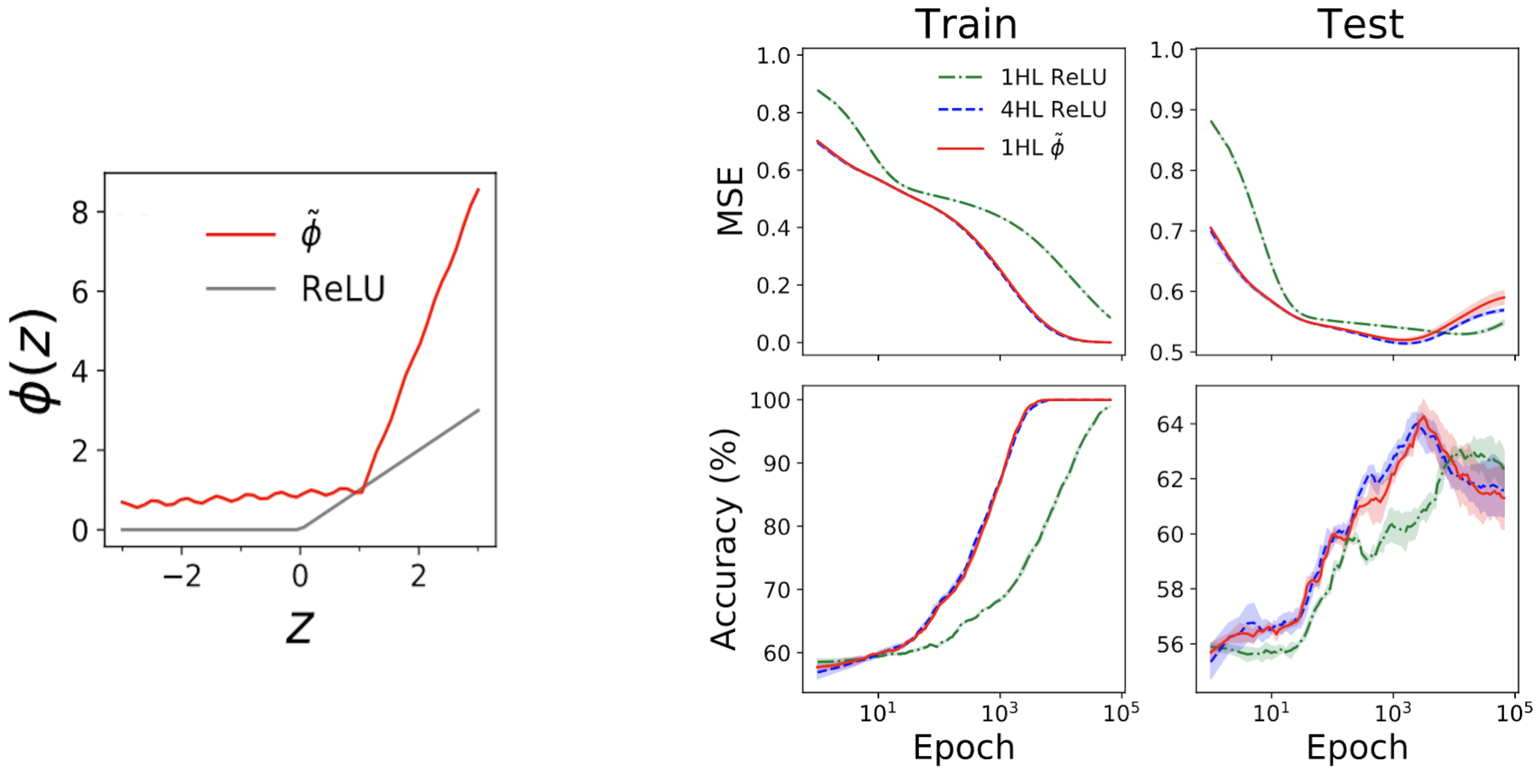
Fig 4. Left panel: our engineered “mimic” activation perform, plotted with ReLU for comparability. Proper panels: efficiency traces for 1HL ReLU, 4HL ReLU, and 1HL mimic FCNs skilled on a UCI dataset. Notice the shut match between the 4HL ReLU and 1HL mimic networks.
That is fascinating from an engineering perspective as a result of the shallow community makes use of fewer parameters than the deep community to realize the identical efficiency.
It’s additionally fascinating from a theoretical perspective as a result of it raises basic questions in regards to the worth of depth.
A standard perception deep studying perception is that deeper just isn’t solely higher however qualitatively totally different: that deep networks will effectively study features that shallow networks merely can’t.
Our shallowification end result means that, at the least for FCNs, this isn’t true: if we all know what we’re doing, then depth doesn’t purchase us something.
Conclusion
This work comes with plenty of caveats.
The largest is that our end result solely applies to FCNs, which alone are not often state-of-the-art.
Nevertheless, work on convolutional NTKs is quick progressing, and we consider this paradigm of designing networks by designing kernels is ripe for extension in some type to those structured architectures.
Theoretical work has to this point furnished comparatively few instruments for sensible deep studying theorists.
We purpose for this to be a modest step in that path.
Even with out a science to information their design, neural networks have already enabled wonders.
Simply think about what we’ll be capable to do with them as soon as we lastly have one.
This submit relies on the paper “Reverse Engineering the Neural Tangent Kernel,” which is joint work with Sajant Anand and Mike DeWeese. We offer code to breed all our outcomes. We’d be delighted to subject your questions or feedback.